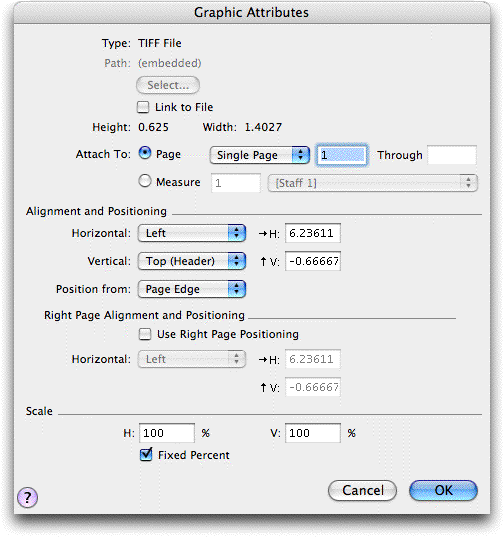

Use the Graphic Attributes dialog box to control the positioning of a graphic in the score, the range of pages a graphic appears on, and whether it is assigned to a measure (in which case the graphic will only appear on the page containing the selected measure), or a page (in which case you can set the graphic to display on one or more pages). If a graphic is displayed on more than one page, changing the attributes for the graphic changes the display of the graphic on all pages.
If you’re using running headers or footers in your score, you might want to position a graphic in the header or footer near the "outside" edges or margins (the left or right edges, respectively) of each left or right page, as opposed to positioning the graphic in the same place on every page. This is easily done using special positioning settings for right-facing pages.
The page number(s) in the Graphic Attributes dialog box may differ between the part and the score if either contains blank/title pages. For example, if there is one title page on the part but not the score and a graphic is assigned to the first page containing music, the Graphic Attributes dialog box indicates page 1 while viewing the score and page 2 while viewing the part.
Note. The Page options are only available when Attach to: Page is selected, because a graphic assigned to a measure can only appear on the page containing that measure.
Note. When you change whether a graphic is assigned to a page or a measure, Finale resets the H: and V: values to zero. It also sets Measure to 1 or Page to 1 (or to the current page if you’re in Page View).
Use the Verticalpop-up list to position a page-assigned graphic vertically. Select Top (Header) or Bottom (Footer) from the pop-up list if you want Finale to place the graphic at a distance measured from the top or bottom of the page edge or margin. Choose Center to center the graphic between the top and bottom of the page. The graphic is positioned vertically between the page margins or the edge of the page, depending on the Position from selection. When you change the vertical alignment, Finale resets the V: setting to zero.
Use the Position from pop-up list to have Finale calculate a page-assigned graphic’s position starting from either the page margin or page edge. Select Page Margin to have Finale measure the graphic’s position starting from the page margin. Select Page Edge to measure the graphic’s position from the page edge. Finale repositions the graphic from the margin or edge; it does not reset the H: and V: settings.
Note. The Horizontal, Vertical and Position from options are only available for page-assigned graphics (Attach to: Page is selected).
Use the H: and V: values to position a measure- or a page-assigned graphic horizontally and vertically. For measure-assigned graphics (Attach to: Measure is selected), enter values in H: and V: to position the graphic from the top-left of the measure, which is the default position if H: and V: are zero. For page-assigned graphics (Attach to: Page is selected), enter values in H: and V: to position the graphic on the page, based on your settings in the Alignment and Positioning group box. In either case, enter a value for H: to change the horizontal position. A positive number moves the graphic to the right; a negative number moves it to the left. Enter a value for V: to change the vertical position. A positive number moves the graphic higher; a negative number moves it lower.
Note. The H: and V: options in the Alignment and Positioning group box are used for both measure- and page-assigned graphics.
Check Fixed Percent to keep the graphic a fixed size even when you change the size of your page with the Resize tool.
Use the Horizontalpop-up list to position page-assigned graphics horizontally on right-facing pages when Use Right Page Positioning is selected. The pop-up list works the same as the Horizontal pop-up list in the Alignment and Positioning group box, but are used for right-facing pages only.
Use the H: and V: values to position page-assigned graphics on right-facing pages when Use Right Page Positioning is selected. These settings work the same as the H: and V: settings in the Alignment and Positioning group box, but are used for right-facing pages only.
Tip. If you're using running headers or footers in your score, you might want to position a graphic as a header or footer near the "outside" edges or margins of each left or right page, as opposed to always distancing the graphic from the left or right page edge (or margin). This is easily done using special positioning settings for right-facing pages. For example, choose Left Pages, and enter 6 Through 10 to display the graphic on every left page between pp. 6-10.
Note. The Page options are only available when Attach to: Page is selected.
See Also:
| User Manual Home |

|