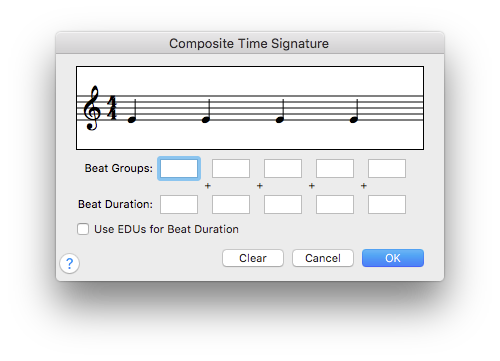
Composite Time Signature dialog box
How to get there
- Choose the Time Signature tool
 , and double-click the measure in which you want to change the meter. The Time Signature dialog box appears.
, and double-click the measure in which you want to change the meter. The Time Signature dialog box appears. - Click Composite. Or, click the Options button and select the Composite button in the expanded options section of the Time Signature dialog box.
What it does
This dialog box allows you to create complex time signatures.
- Beat Groups: _ + _ + _ + _ + _ . Enter up to five numbers that you want to appear as the upper half of the composite time signature, specifying the number of beats per measure. Finale treats each number and its corresponding Beat Duration as a separate component of the composite time signature. You can use + signs between numbers within a text box if you need time signatures such as 3+2+2 over 8 You can also use decimals, such as .75.
- Beat Duration: _ + _ + _ + _ + _ . Enter up to five numbers you want to appear as the lower half of a composite time signature. These numbers specify the rhythmic value of the beats in the measure. Each number appears below its corresponding Beat Group number. You can use + signs between numbers within the Beat duration text box.
- Use EDUs for Beat Duration. Select this check box if you need to enter beat durations for dotted notes. When this check box is selected, Finale uses the specified
 EDUsEDUs, or ENIGMA Duration Units, are Finale's high-resolution measurement for the duration of notes and rests, defined as 1024 EDUs per quarter note. number for the beat duration. When this check box is not selected, Finale displays the number you enter in the lower half of the composite time signature.
EDUsEDUs, or ENIGMA Duration Units, are Finale's high-resolution measurement for the duration of notes and rests, defined as 1024 EDUs per quarter note. number for the beat duration. When this check box is not selected, Finale displays the number you enter in the lower half of the composite time signature. - OK • Cancel • Clear. Click OK to save new settings and return to the score, or click Cancel to cancel any changes you made to the settings. Click Clear to remove the current composite time signature settings.
Tip: As an example, a dotted quarter can be specified as the beat duration by entering 1536: 1024 ![]() EDUsEDUs, or ENIGMA Duration Units, are Finale's high-resolution measurement for the duration of notes and rests, defined as 1024 EDUs per quarter note. (quarter note) plus 512 EDUs (eighth note).
EDUsEDUs, or ENIGMA Duration Units, are Finale's high-resolution measurement for the duration of notes and rests, defined as 1024 EDUs per quarter note. (quarter note) plus 512 EDUs (eighth note).
See also:


