How to get there
This dialog box is displayed any time you click a Set Font button. You can find a Set Font button in, for example, the Measure Number, Articulation Designer, and Expression Designer dialog boxes.
What it does
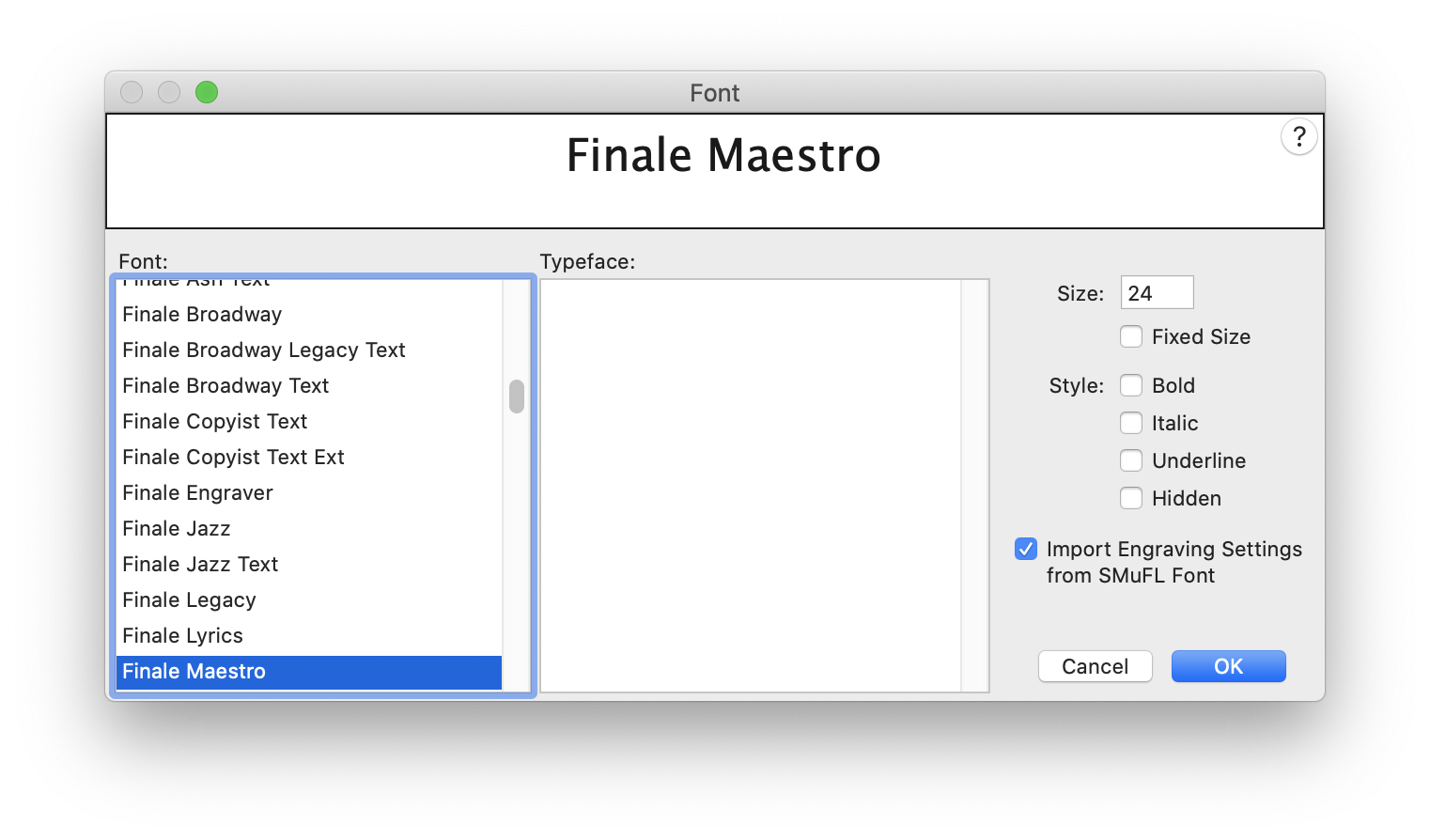
In this dialog box you can specify a font (typeface), point size, and style for the text element you’re defining. Finale displays sample text to show the effects of your selection.
- Font. In this scrolling alphabetical list, Finale displays every font installed. Click a font name to select it. If any elements in the score use fonts that were present when the document was created or edited, but are no longer installed, then the font name appears in the Font text box but not in the scrolling font list; see Font Utilities dialog box. At the top of the dialog box, Finale shows you the actual text you’ve typed, if appropriate. Enter the Size (and click each check box to remove any dashes) to preview the selected font. (A dash indicates the current fixed size or style specified for any text existing in the document. Because more than one size/style may exist in the document for any given font, the font preview is only available with dashes removed.)
- Size. In this text box, enter the size, in points (72 per inch), for the textual element you’re designing. Each time you enter a number, Finale updates the sample text display to reflect the change. See Fonts for some important advice about selecting fonts and type sizes.
- Fixed Size. Normally, when you use the Resize tool to make your music larger or smaller on the page, Finale scales all page elements by the same amount, including text. Therefore, the size of your lyrics and titles, for example, always remains proportional to the music around it.
In some cases, though, you may want to specify a point size for some text that will never change, even if you reduce or enlarge the music on the page (lyrics and titles are the most common examples). If that’s the case, select Fixed Size; Finale won’t scale this text if the size of the music changes.
- Style. Click as many of these check boxes as you want; each creates a stylistic change in the font and size you’ve selected, as follows: Bold, Italic, Underline, and Hidden.
- Import Engraving Settings from SMuFL Font. This option is only available when a SMuFL-compliant music font is selected to be used as the default music font for a document. This will import the SMuFL-based engraving defaults associated with the selected font. It is recommended to keep this box selected. For more details see Engraving Defaults.
- OK • Cancel. Click OK to confirm, or Cancel to discard, the font change you’ve specified. You return to the previous dialog box.
Noteman says: When you’re creating musical elements such as Articulations, Finale conveniently displays the default music font at the top of the list (usually Maestro) as well as in its normal alphabetical position.
See also:


